) = (1 + 8
^2^4t^2/s_0^2)^-1/2,
(2)I have fitted several functional forms for the depolarization behaviour to the data. A Burn (1966) depolarization law does not fit the data well. A depolarization law of the form
p() = (1 + 8^2^4t^2/s_0^2)^-1/2,
(2)
gives a reasonable fit to the data in many cases, where s_0 is the scale of the RM fluctuations and t the resolution (Tribble 1991). The only discrepancies are where the polarization falls slightly faster than equation (2) predicts. This isn't a problem, as equation (2) and the Burn depolarization law are the two limiting cases of a foreground screen with RM structure on scales very much larger and very much smaller than the observing beam respectively. A family of depolarization laws can then be considered, (Tribble 1991)
p^2(,s_0/t)
= [1 - exp(-s_0^2/2t^2-4^2^4) / 1 +
8^2^4t^2/s_0^2]
+ exp(-s_0^2/2t^2-4^2^4) (3)
from which the Burn and well-resolved depolarization laws are recovered
in the limits s_0/t->0 and s_0/t->
.
Essentially, for a given long wavelength polarization, the polarization
at short wavelengths is increased by an amount depending on the
effective resolution s_0/t.
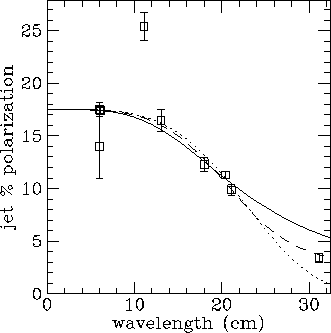
Fig 1a. The polarization of the jet side of 3C9, together with
depolarization laws for the three cases s_0/t=0, 0.8, . The
Burn law is a dotted line, the well resolved screen a solid line, and
the dashed line shows an intermediate case. The case with s_0/t=0.8
gives the best description.
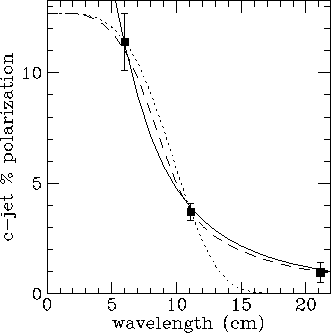
Fig 1b. The polarization of the counterjet side of 3C133, together with
depolarization laws for the three cases s_0/t=0, 0.8, . The
Burn law is definitely excluded but a variety of s_0/t are
allowed.
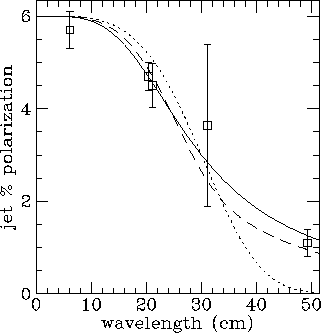
Fig 1c. The polarization of the jet side of 3C200, together with
depolarization laws for the three cases s_0/t=0, 1, . The
Burn law is definitely excluded but a variety of s_0/t are
allowed.
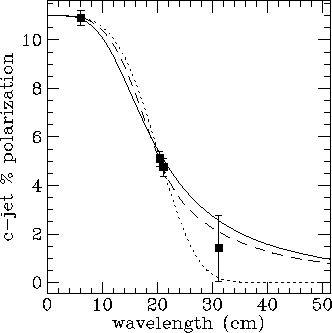
Fig 1d. The polarization of the counterjet side of 3C200, together with
depolarization laws for the three cases s_0/t=0, 1, . All
models are allowed by the data.
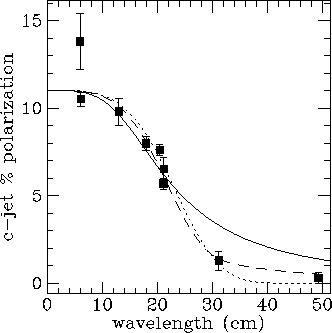
Fig 1e. The polarization of the counterjet side of 3C334, together with
depolarization laws for the three cases s_0/t=0, 0.45, . A
well resolved screen is excluded.
In Figs 1a-e I show some examples of depolarization behaviour together
with different depolarization laws. In general, the polarization
behaviour is consistent with s_0/t being approximately unity.
There are cases where the Burn law fits the data, but in most such
cases the errors on the long wavelength polarization are large. In most
cases the data can rule out either the Burn law or a well resolved
screen, except on the counterjet side of 3C200, but only on the jet
side of 3C9 can both extremes be ruled out. There are other sources
(not shown) with more erratic polarization behaviour. Given sufficient
data over a range of wavelengths, it should be possible to derive both
the RM dispersion and the scale
length s_0.