(1+z)^{-2} n_e B.dl, (4)The RM is
RM = 810 (1+z)^{-2} n_e B.dl, (4)
where n_e is the electron density per cm^3, B is the
magnetic field in 
and l
the path length in kpc. The factor (1+z)^-2 where z
is the redshift of the intervening material allows for the fact that
the wavelength where rotation occurs differs from that observed. The RM
distribution can be described statistically by the RM autocorrelation
function 
(s),
(s) =
<RM(x) RM(x+s)>, (5)
where x are coordinates on the sky and s the projected separation.
The RM autocorrelation function is
(s) =
(1+z)^{-4} < 810^2
dzdz' n_e(z)n_e(z')
B_z(x,z)B_z(x+s,z')>,
(6)
and the <...> can be taken inside the integral and applied to the
magnetic field only to give the magnetic field autocorrelation function
<B_z(x,z)B_z(x+s,z')> 
R_zz (Batchelor 1953). R_ij is an isotropic second
order tensor that may conveniently be written in terms of normalized
longitudinal and lateral correlation functions f and
g,
R_ij(r)= (<B^2>/3)[(f-g / r^2)r_ir_j +
g
_ij], (7)
where r^2=s^2+(z-z')^2. The constraint 
.B=0
implies that g=f+rf'/2. R_zz may therefore be written
as
R_zz(s,z-z')= (<B^2>/3) [f+(s^2/2r)(df/dr)]. (8)
Further progress relies on knowledge of the form of the longitudinal correlation function f. Ideally, this would be determined from the data. Failing this, I use a Gaussian as an illustration,
f(r) = exp(-r^2/2r_0^2). (9)
If r_0 is small then the Gaussian can be approximated by a Dirac delta function which can be integrated out,
(s)
= 
(2
810^2 /
3(1+z)^4) dz
n_e^2(z) <B^2> r_0 exp(-s^2/2r_0^2)[1-(s^2 /
2r_0^2)], (10)
where n_e, B and r_0 are functions of
cluster radius R. When s=0, 
^2 =
<RM^2> = (0) is given as a
function of projected radius S,
^2 = (2 810^2
/ 3(1+z)^4) dz
r_0n_e^2<B^2>. (11)
Assuming that the electron density, magnetic field strength and scale
length vary as power laws of radius, so that
n_e=n_0(R/R_0)^(-m_n), B=B_0(R/R_0)^(-m_b), and
r_0=
_0(R/R_0)^(m_r),
gives
^2 = (2 810^2
/3(1+z)^4) _0 R_0
B_0^2 n_0^2 (S/R_0)^{-2m_n-2m_b+m_r+1} dx
(1+x^2)^{-m_n-m_b+m_r/2} (12)
where x=z/S. The above procedure does not depend on the choice
of f - any function forming a -sequence will
give the same result, to within a constant factor of order unity.
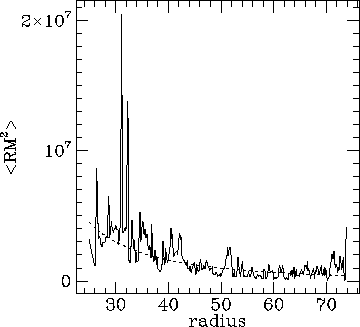
Fig 2. The mean square RM for the west lobe of Cygnus A. The dotted line is the best fit power law with m=1.1.
In equation (12) only the integral differs between the two sides of a
source (assuming, for simplicity, that the scale lengths are the same).
Defining m=m_n+m_b-m_r/2-1/2, then ~
S^-m. All that is now needed is an estimate of the index
m. In Fig. 2 I show <RM^2> as a function of radius in
the west lobe of Cygnus A (the east lobe has larger RMs but is
depolarized and the radial range of the data is much smaller). Also
shown is the best fit power law with m=1.1, which was fitted
after removing isolated pixels and features such as the radio-quiet
bowshock (Carilli, Perley & Dreher 1988). This power law is not a
strong result as the RM distribution is poorly sampled and a mean trend
is also present. It does, however, give a substantially weaker RM
variation than predicted by Soker & Sarazin (1990), and is
consistent with isotropic flux-freezing in a n_e~1/r
inflow.
If the source is at an angle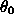 
to the plane
of the sky then the RM dispersion in the front (+) and back (-) lobes
are given by
_
^2 ~
S^{-2m} _{}^{/2} (cos
)^{2m-1}d.
(13)
I define the dispersion ratio D as the ratio _+/_-.
This is tabulated for some values of m in Table 1. I will take
m=1 which fits the available data and is simple to use.
m D
0.5
Table 1. The dispersion ratio D as a function of the
angle 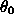of the
source axis to the plane of the sky for different values of the power
law index m.